本文是笔者研究 osu! 戳泡泡模式 PP 算法的一个记录文章，旨在帮助其他对 PP 算法感兴趣的玩家快速建立对 PP 算法的认知。由于大部分内容是笔者的个人理解和经验谈，可能存在错误或者偏差，欢迎读者提出改进意见和补充内容.

本文的代码片段来源于 rosu-pp, rosu-pp 是 osu!lazer 全模式算法的 Rust 实现，也是目前最流行的 PP 计算库。本文面向略有编程经验的读者，读者不必深入了解 Rust, 只需要具有本科级别的编程知识和数学知识即可理解本文内容.

# 初探 PP 算法

# 两步式计算

抛开复杂的算法不谈，我们先来谈论一些表象。在表面来看，PP 系统会综合评估谱面难不难和打的好不好两个概念，最终计算出一个 PP 数值.

广泛存在的一个误区是 PP 系统会根据 Replay 来评判这两个概念，这是一种错误的认知。实际上，PP 计算是两步式进行的，第一步计算谱面难度 (这一步通常自变量是所有物件和速度倍率), 第二步是根据第一步算出的谱面难度和以及一些其他变量 (例如谱面的三维，玩家 Acc, Miss 数，最大 Combo) 共同计算出最终 PP 数值.

不难想象，第一步计算的时候我们主要在考虑物件之间相互影响产生的基值，而第二步计算主要是根据玩家的表现在基值上进行倍率的调整。这里我们举一个简单的例子，曲奇在 FDFD 中取得了 939PP 的成绩，而 mrekk 取得了 926PP 的成绩，Accolibed 取得了 640PP 的成绩，他们三人在第一步计算中算出的基值是相同的，只是在第二步计算中产生了不同的倍率。曲奇的准确度高于 mrekk, 固取得了更高的 acc_bonus. Accolibed 掉了一个 Miss, 固得到了 miss_penalize. 最终形形色色的 bonus 和 penalize 在第二步作用在基值上，算出了最终的数值.

也正因如此，在利用各种 PP 计算器来计算大量成绩的时候，先按照谱面归类将大幅提高计算效率，因为在没有开启调整速度的 Mod 的情况下，第一步计算 (这也是决速步骤) 只用进行一次就足够了.

上文提到的误区实际上源自于玩家对算法的过度期待: Miss 了简单的部分，SS 了困难的部分，PP 算法是无法分辨出这两个场景的。这些场景只能被视为一个整体，表现于上文提到的其他变量中，影响第二步计算的各种倍率。这也是各个 PP 计算器不需要提供 Replay, 只需要提供最终结果，就能计算出准确 PP 的原理所在.

至此，我们已经将 PP 计算的过程分为了两部分，通常来说，第一步被称为 Difficulty 计算，第二步被称为 Performance 计算.

# Difficulty 与 Skills

经过上文的探究，我们明白了 Difficulty 的计算是重中之重，是区分谱面难不难的关键.

osu! 的设计者们有意识地从多个维度来评估谱面的难度，在多年的逐步迭代中明确了 Skills 这个概念。当然，针对不同的模式，Skill 分别有不同维度的定义.

对于戳泡泡玩家而言，戳泡泡模式的 Skills 应该至少包含了 Aim 和 Speed 这两个老生常谈的维度，当然事实也是这样的，可以参考下面的表格.

• osu!standard: Aim, Speed, Flashlight
• osu!mania: Strain
• osu!catch: Movement
• osu!taiko: Color, Rhythm, Stamina

这里由于笔者对其他模式不甚了解，这里我们主要将目光聚焦于 osu!standard. 本文主要也将谈论 Aim, Speed 两个 Skill.

# Skill 与 微积分？

相信读者读到这里已经对 Aim, Speed 的具体计算非常感兴趣了，但在正式开始之前，我们先笼统地认识一下 Skill 的计算方式.

读者不妨设想一下，对于一张时长几分钟的谱面，我们应该如何计算他的难度呢？实际上这个问题是困难的，物件以时间为轴堆叠仅仅是一堆表示位置的数组，是很难衡量困难与否的。如果在本科期间修读过高等数学的读者可能对这个例子感到熟悉：一个光滑的曲面本身可能是不规则的，想要计算面积是很困难的，但是如果将曲面无限细分，将最小单位看作是一个正方体，问题就很好解决了。即整体的求解是困难的，但是一个切片往往是容易求解的.

Skill 的计算遵循了类似先微分后积分的过程，在计算过程中，物件被细分进行单独对待.

简单来说，每个物件都可以算作一个表示难度的元素，在 PP 系统中，这个元素被称作是 Strain. 某 Skill 数值的计算依托于一个 Strain 构成的集合。最终 Skill 数值 (例如: raw_aim, raw_speed), 实际上是对 Strains 进行积分 (以某种方式累加) 的结果.

戳泡泡中，大部分 Pattern (例如：锐角跳，钝角跳) 都是针对 Strain 展开的，即我们在计算单个 Strain 的过程中区分这些 Pattern, 并给出最终的 Strain 值。在实际计算 Strain 的过程中，我们可以拿到很多参数辅助我们，决定 "当前物件的难度".

• osu_curr_obj, osu_last_obj, osu_last_last_obj: 拿到前后的物件
• travel_dist, travel_time, strain_time, jump_dist: 距离，时间等几何量、物理量

我们会在之后的讲解中逐步接触和理解这些概念。在之后的讲解中，我们也将以 Strain 计算为重点，自下而上地剖析具体计算过程.

接下来，我们将逐步探寻 Aim, Speed 两个 Skill, 并且尝试阅读单个 Strain 是如何被计算的.

# 探索 Aim Skill

在 rosu-pp 中，我们可以在 /osu/difficulty/skills 目录找到所有 Skill 的定义和实现。这里我们尝试开始阅读 aim.rs 的源代码

impl<'a> Skill<'a, Aim> {

    fn strain_value_at(&mut self, curr: &'a OsuDifficultyObject<'a>) -> f64 {

        self.inner.curr_strain *= strain_decay(curr.delta_time, STRAIN_DECAY_BASE);

        self.inner.curr_strain +=

            AimEvaluator::evaluate_diff_of(curr, self.diff_objects, self.inner.with_sliders)

                * SKILL_MULTIPLIER;

        self.inner.curr_strain

    }

}

在针对 Skill<'a, Aim> 的实现中，最吸引我们注意的是 strain_value_at 方法，因为 curr_strain 值正是从这里发源的.

在上文的解释中，我们已经明确了一个概念：在计算过程中，物件被细分进行单独对待.

所以显然， strain_value_at 会被调用多次，其参数 curr 表示将要被计算的某一物件， self.diff_objects 是所有物件列表的一个引用.

self.diff_objects 的存在是必要的，因为在计算单个物件的时候，我们需要获取该物件的上下文.

	pub trait IDifficultyObject: Sized {
	fn idx(&self) -> usize;
	fn previous<'a, D>(&self, backwards_idx: usize, diff_objects: &'a [D]) -> Option<&'a D> {}
	fn next<'a, D>(&self, forwards_idx: usize, diff_objects: &'a [D]) -> Option<&'a D> {}
	}

简单阅读 IDifficultyObject 的定义，相信读者已经明白 idx , diff_objects 的必要性和使用场景了.

接下来，我们将目光放到 AimEvaluator::evaluate_diff_of 方法上，我们将按行分块解释这个方法.

# osu_curr_obj

let osu_curr_obj = curr;

let Some((osu_last_last_obj, osu_last_obj)) = curr

    .previous(1, diff_objects)

    .zip(curr.previous(0, diff_objects))

    .filter(|(_, last)| !(curr.base.is_spinner() || last.base.is_spinner()))

else {

    return 0.0;

};

这部分主要负责解构出 osu_curr_obj , osu_last_obj , osu_last_last_obj .

利用 diff_objects 和对象储存的物件 ID 就可以还原出上一个物件与下一个物件.

这里很明显地，当物件为转盘 (Spinner) 时，方法将直接返回 0.0, 不执行后续计算.

# 距离 / 时间 = 速度

// * Calculate the velocity to the current hitobject, which starts

// * with a base distance / time assuming the last object is a hitcircle.

let mut curr_vel = osu_curr_obj.lazy_jump_dist / osu_curr_obj.strain_time;

// * But if the last object is a slider, then we extend the travel

// * velocity through the slider into the current object.

if osu_last_obj.base.is_slider() && with_sliders {

    // * calculate the slider velocity from slider head to slider end.

    let travel_vel = osu_last_obj.travel_dist / osu_last_obj.travel_time;

    // * calculate the movement velocity from slider end to current object

    let movement_vel = osu_curr_obj.min_jump_dist / osu_curr_obj.min_jump_time;

    // * take the larger total combined velocity.

    curr_vel = curr_vel.max(movement_vel + travel_vel);

}

// * As above, do the same for the previous hitobject.

let mut prev_vel = osu_last_obj.lazy_jump_dist / osu_last_obj.strain_time;

if osu_last_last_obj.base.is_slider() && with_sliders {

    let travel_vel = osu_last_last_obj.travel_dist / osu_last_last_obj.travel_time;

    let movement_vel = osu_last_obj.min_jump_dist / osu_last_obj.min_jump_time;

    prev_vel = prev_vel.max(movement_vel + travel_vel);

}

let mut wide_angle_bonus = 0.0;

let mut acute_angle_bonus = 0.0;

let mut slider_bonus = 0.0;

let mut vel_change_bonus = 0.0;

// * Start strain with regular velocity.

let mut aim_strain = curr_vel;

这部分的主要逻辑是利用距离除以时间算出速度，并且把速度当做初始 aim_strain 值.

这里我们解释一些基本概念，以便于具体理解这些参数:

# strain_time

表示当前物件与上一物件的时间间隔，单位为毫秒.

计算方式为: 当前物件的起始时间 - 上一物件的起始时间 .

也可以用下面的这种方式进行计算: (60 / BPM) * 节拍细分 * 1000 .

对于大部分谱面，符合下面这样的例子:

• 对于 180BPM 的跳: (60 / 180) * 1/2 * 1000 = 166.67ms.
• 对于 180BPM 的串: (60 / 180) * 1/4 * 1000 = 83.34ms.
• 对于 200BPM 的跳: (60 / 200) * 1/2 * 1000 = 150.00ms.
• 对于 200BPM 的串: (60 / 200) * 1/4 * 1000 = 75.00ms.

算法中规定，MIN_DELTA_TIME = 25.0, 即 strain_time 的最小值为 25ms.

关于节拍细分的更多内容可以查看 osu!Wiki: 音符时值 (Beat Snap Divisor)

# lazy_jump_dist

表示当前物件与上一物件的标准化距离，单位为 osu!pixel

计算方式为: normalize(||当前物件的位置 - 上一物件的位置||)

osu!pixel 的区域为 (0, 0) 到 (512, 384), 在实际游玩中会根据分辨率进行缩放.

物件的位置会进行标准化，标准化的时候，取圆圈物件的半径为 50 单位长度，注：此时会考虑 CS.

同时也与作图的堆叠度配置有关，感兴趣的读者可以自行阅读相关代码

# travel_dist

表示滑条物件的滑行距离

# travel_time

表示滑条物件的滑行时间

# min_jump_time

表示刨除滑行时间后，当前物件与上一滑条头之间的时间间隔.

通常在上一物件为滑条的情形下使用，如果上一物件不是滑条，该值与 strain_time 相等.

# min_jump_dist

表示刨除滑行距离后，当前物件与上一滑条尾之间的距离.

通常在上一物件为滑条的情形下使用，如果上一物件不是滑条，该值与 lazy_jump_dist 相等.

接下来我们返回到代码解析部分，相信读者最感兴趣的就是 extend velocity 这部分，我们画图来解释一下

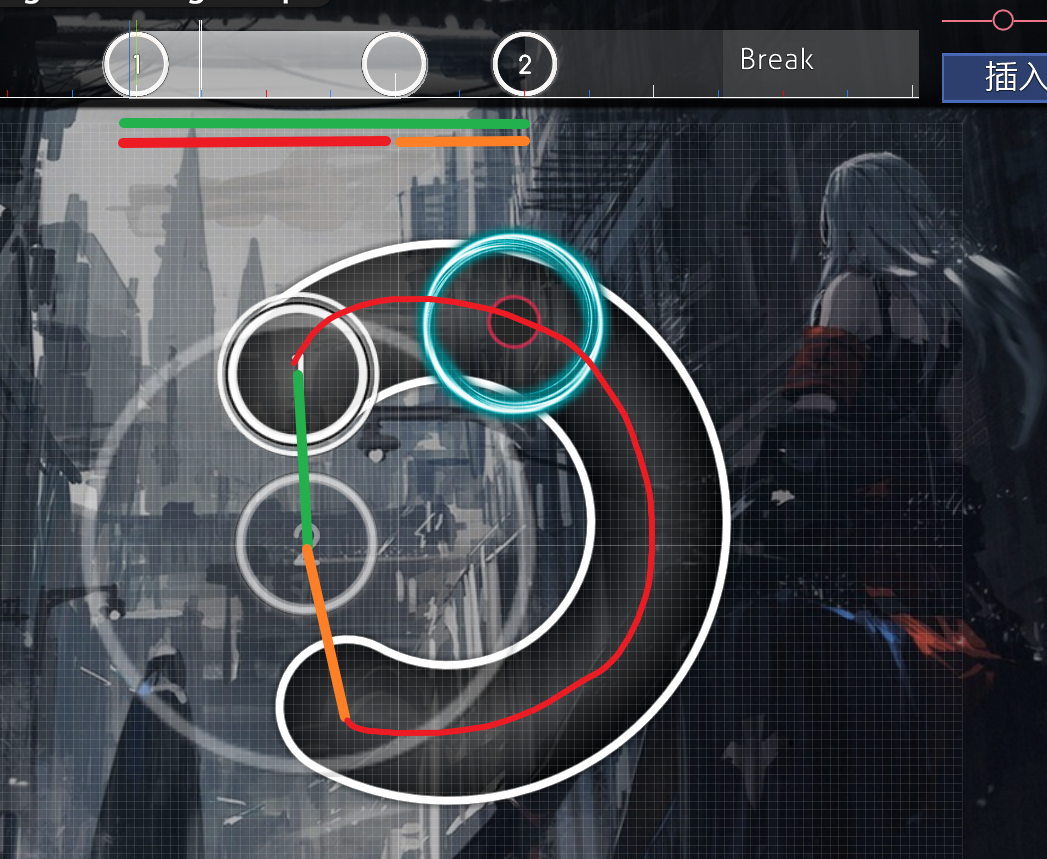
请读者将圆圈 2 当做当前物件，很明显，绿色的是第一步计算的 curr_vel , 接下来，进入 if 逻辑的判断.

因为上一个物件是滑条，条件满足，这里接下来会分别计算红色部分和橘色部分的速度，并且求和，与原 curr_vel 取最大值.

很明显，对于图中这种排列，红色部分和橘色部分的速度和是大于绿色的，故采用后续计算出的值作为 curr_vel .

这里客观来讲，extend velocity 更能表现出滑条 1 与圆圈 2 组合的速度.

# 锐角与广角排列

在上一部分，我们根据速度计算出了 Strain 的基础值，接下来 PP 算法考虑了经典的锐角和钝角 Pattern, 计算出了有针对性的奖励系数.

注：此处的代码经过了一些删减、重新排序和提取，在不改变逻辑的情况下提升了可读性.

这里我们按照注释，将代码分为四部分：节奏判断、基础值计算、锐角增益计算、重复惩罚.

// * If rhythms are the same (节奏判断).

if osu_curr_obj.strain_time.max(osu_last_obj.strain_time)

    < 1.25 * osu_curr_obj.strain_time.min(osu_last_obj.strain_time)

{

    // * Rewarding angles, take the smaller velocity as base (基础值计算).

    let angle_bonus = curr_vel.min(prev_vel);

    wide_angle_bonus = Self::calc_wide_angle_bonus(curr_angle);

    acute_angle_bonus = Self::calc_acute_angle_bonus(curr_angle);

    // * Only buff deltaTime exceeding 300 bpm 1/2 (锐角增益计算).

    if osu_curr_obj.strain_time > 100.0 {

        acute_angle_bonus = 0.0;

    } else {

        let base1 =

            (FRAC_PI_2 * ((100.0 - osu_curr_obj.strain_time) / 25.0).min(1.0)).sin();

        let base2 = (FRAC_PI_2

            * ((osu_curr_obj.lazy_jump_dist).clamp(50.0, 100.0) - 50.0)

            / 50.0)

            .sin();

        // * Multiply by previous angle, we don't want to buff unless this is a wiggle type pattern.

        acute_angle_bonus *= Self::calc_acute_angle_bonus(last_angle)

        // * The maximum velocity we buff is equal to 125 / strainTime

            * angle_bonus.min(125.0 / osu_curr_obj.strain_time)

            // * scale buff from 150 bpm 1/4 to 200 bpm 1/4

            * base1.powf(2.0)

                // * Buff distance exceeding 50 (radius) up to 100 (diameter).

            * base2.powf(2.0);

    }

    // * (重复惩罚)

    // * Penalize wide angles if they're repeated, reducing the penalty as the lastAngle gets more acute.

    wide_angle_bonus *= angle_bonus

        * (1.0

            - wide_angle_bonus.min(Self::calc_wide_angle_bonus(last_angle).powf(3.0)));

    // * Penalize acute angles if they're repeated, reducing the penalty as the lastLastAngle gets more obtuse.

    acute_angle_bonus *= 0.5

        + 0.5

            * (1.0

                - acute_angle_bonus

                    .min(Self::calc_acute_angle_bonus(last_last_angle).powf(3.0)));

}

# 节奏判断

在最外层进行了节奏的判断，只有符合条件的物件会得到额外的 Bonus. 这里主要是锐角和广角的 Bonus.

首先，算法先保证了节奏变化幅度不大，限制当前物件与上一物件的间隔时间变化在 25% 以内.

在客观角度考虑，Pattern 存在的必要条件就是节奏变化幅度较小。如果节奏变化太大就不能称为是 Pattern 了.

# 基础值计算

wide_angle_bonus = Self::calc_wide_angle_bonus(curr_angle);

acute_angle_bonus = Self::calc_acute_angle_bonus(curr_angle);

fn calc_wide_angle_bonus(angle: f64) -> f64 {

    (3.0 / 4.0 * ((5.0 / 6.0 * PI).min(angle.max(PI / 6.0)) - PI / 6.0))

    .sin()

    .powf(2.0)

}

fn calc_acute_angle_bonus(angle: f64) -> f64 {

    1.0 - Self::calc_wide_angle_bonus(angle)

}

接下来，算法根据物件之间角度的数值，计算出了广角和锐角增益的基础值，范围为 0 ~ 1.

((5.0 / 6.0 * PI).min(angle.max(PI / 6.0)) - PI / 6.0) 计算了角度与 π/6 的偏移值.

3/4 * 偏移值 是在对定义域进行伸缩，伸缩到 (30, 150).

sin²(偏移值) 将结果限制到 0 ~ 1 之间

使用 GeoGebra 可以画出下面这样的曲线，红线代表广角曲线，蓝色代表锐角曲线.

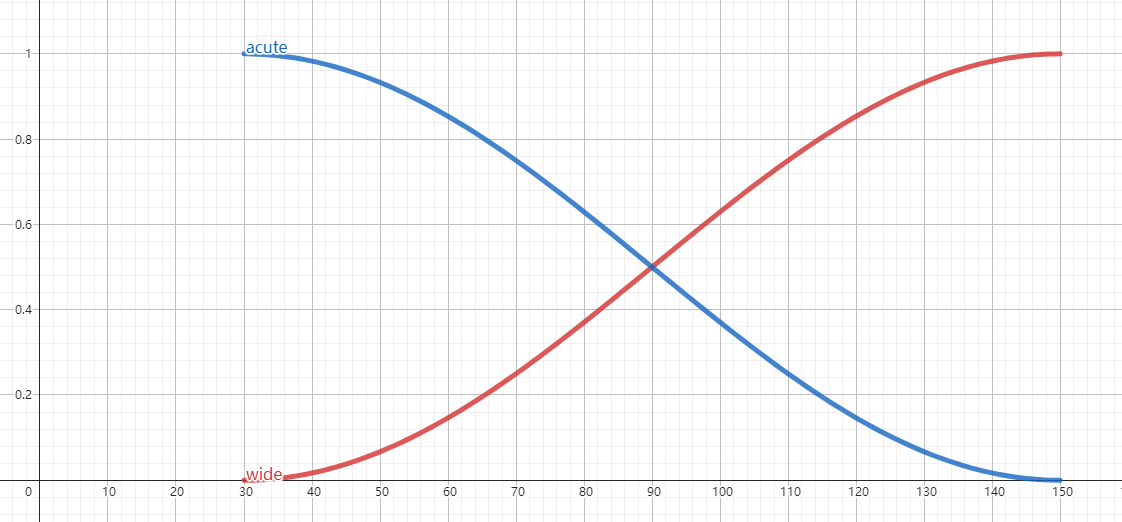
在客观角度考虑，30 度以上，广角增益系数随角度平滑增长. 150 度以下，锐角增益系数随角度平滑增长，是很自然的设计.

很明显地，算法有意将 30 度以下的角度视作锐角，将 30 度以上的角度视为广角，我们常说的直角、钝角 Pattern 实际上都归属于广角的领域.

# 锐角增益计算

首先，锐角增益中 osu_curr_obj.strain_time > 100.0 限制了只有 300BPM 以上的跳或者 150BPM 以上的串会被增益.

这意味着大部分的排列不会吃到锐角增益。这个结论很有意思，也很符合逻辑. 300BPM 以上的跳不必多说了.

这里 150BPM 的串看似几乎没有限制，但是请读者考虑一下，小于 90 度的串甚至已经进入了 aim control 的领域了.

可能有读者对 acute_angle_bonus 置为 0 有疑问，在下文的讲解中，这个顾虑便会消失.

实际上，最终增益系数的值是选取锐角和广角增益的较大者，也就说一个物件要么被认为是广角、要么被认为是锐角.

let base1 =

    (FRAC_PI_2 * ((100.0 - osu_curr_obj.strain_time) / 25.0).min(1.0)).sin();

let base2 = (FRAC_PI_2

    * ((osu_curr_obj.lazy_jump_dist).clamp(50.0, 100.0) - 50.0)

    / 50.0)

    .sin();

// * Multiply by previous angle, we don't want to buff unless this is a wiggle type pattern.

acute_angle_bonus *= Self::calc_acute_angle_bonus(last_angle)

// * The maximum velocity we buff is equal to 125 / strainTime

    * angle_bonus.min(125.0 / osu_curr_obj.strain_time)

    // * scale buff from 150 bpm 1/4 to 200 bpm 1/4

    * base1.powf(2.0)

    // * Buff distance exceeding 50 (radius) up to 100 (diameter).

    * base2.powf(2.0);

这里英文注释为我们理解提供了极大便利.

首先 *= Self::calc_acute_angle_bonus(last_angle) , 这个操作实际上在规避 "离群值".

这里注释中提到，只希望考虑摇摆型的锐角，摇摆型可以理解为：连续的几个物件都符合锐角的特征.

而偶然性的，突发性的锐角不在增益范围，这也是合情合理的，这种突发性的锐角不应被视作 Pattern.

接着，对 velocity, strain_time, distance 分别进行了伸缩.

base1 的增益范围为: 150 ~ 200BPM 的串 (1/4 节拍)

base2 的增益范围为: 50 ~ 100 单位 (互过圆心的物件～相切的物件)

# 重复惩罚

// * Penalize wide angles if they're repeated, reducing the penalty as the lastAngle gets more acute.

wide_angle_bonus *= angle_bonus

    * (1.0

        - wide_angle_bonus.min(Self::calc_wide_angle_bonus(last_angle).powf(3.0)));

// * Penalize acute angles if they're repeated, reducing the penalty as the lastLastAngle gets more obtuse.

acute_angle_bonus *= 0.5

    + 0.5

        * (1.0

            - acute_angle_bonus

                .min(Self::calc_acute_angle_bonus(last_last_angle).powf(3.0)));

经过逻辑分析后，我们可以将惩罚的关键部分抽象为 1.0 - f(x) , f (x) 的增大意味着受到更大的惩罚.

这里通过比较上一个 Bonus, 可以间接地对重复的广角进行惩罚，如果上一个角度更锐，惩罚因子 f (x) 会减小，从而对重复的广角施加更轻微的惩罚.

min() 选择较小的值作为惩罚因子，这个比较是为了确保惩罚因子不会超过 wide_angle_bonus 的值.

# 速度变化

上一部分我们针对锐角和广角排列进行了奖励，其前提是速度相近，即速度变化在 25% 以内.

下面我们将引入速度变化奖励，这次与上文有着相反的前提，即速度一定要有不同，我们将采用与上一节类似的策略来分析.

这里我们按照注释，将代码分为三部分：比率计算、基数计算、节奏变化惩罚.

if prev_vel.max(curr_vel).not_eq(0.0) {

    // * (比率计算)

    // * We want to use the average velocity over the whole object when awarding

    // * differences, not the individual jump and slider path velocities.

    prev_vel = (osu_last_obj.lazy_jump_dist + osu_last_last_obj.travel_dist)

        / osu_last_obj.strain_time;

    curr_vel =

        (osu_curr_obj.lazy_jump_dist + osu_last_obj.travel_dist) / osu_curr_obj.strain_time;

    // * Scale with ratio of difference compared to 0.5 * max dist.

    let dist_ratio_base =

        (FRAC_PI_2 * (prev_vel - curr_vel).abs() / prev_vel.max(curr_vel)).sin();

    let dist_ratio = dist_ratio_base.powf(2.0);

    // * Reward for % distance up to 125 /strainTime for overlaps where velocity is still changing. (基数计算)

    let overlap_vel_buff = (125.0 / osu_curr_obj.strain_time.min(osu_last_obj.strain_time))

        .min((prev_vel - curr_vel).abs());

    vel_change_bonus = overlap_vel_buff * dist_ratio;

    // * Penalize for rhythm changes. (节奏变化惩罚)

    let bonus_base = (osu_curr_obj.strain_time).min(osu_last_obj.strain_time)

        / (osu_curr_obj.strain_time).max(osu_last_obj.strain_time);

    vel_change_bonus *= bonus_base.powf(2.0);

}

# 比率计算

在代码的后半部分，我们可以看到 vel_change_bonus = overlap_vel_buff * dist_ratio .

即最终速度变化奖励是利用 基数 * 比率 的方式进行计算的，这里我们先来看比率的计算方式.

首先，针对 prev_vel 和 curr_vel 进行了重算，使用了之前图 1 中绿色的部分作为速度值.

接下来， dist_ratio 与上文计算角度奖励的方式类似，都采用先正弦再平方的方式，很明显地， dist_ratio 的取值范围为 [0, 1]

(prev_vel - curr_vel).abs() / prev_vel.max(curr_vel) 计算了速度变化的大小相对于最大速度的比例，反应了速度变化的剧烈程度.

速度变化的剧烈程度作为速度奖励的比率，在合适不过了.

(a - b).abs () /a.max (b) 是一种特征缩放方式，可以将任意量纲的数值范围缩放到 [0, 1] 区间里.

这里 x, y 可分别看作当前物件与上一物件的速度，而 z 值则为归一化后的速度变化.

上文两次提到的先正弦再平方实际上也是一种特征映射的方式，可以将原始值 x 映射到 [0, 1] 的范围内，并且平方操作可以增强映射后的值的变化幅度.

这里考虑到的变化幅度，读者不妨考虑正弦函数各点的斜率 (导数), 其变化幅度便一目了然了.

# 基数计算

很明显，这里直接使用了速度变化的大小作为基数的值.

(prev_vel - curr_vel).abs() 计算了前后两个物件的速度大小的差值.

(125.0 / osu_curr_obj.strain_time.min(osu_last_obj.strain_time)) 主要是限制了距离对速度的影响.

限制可以确保在计算速度变化时，只考虑在一定范围内的速度变化。使奖励值更加关注较近的对象之间的速度变化，而忽略较远对象之间的变化.

# 节奏变化惩罚

这里节奏变化惩罚也运用了类似的归一化手段. bonus_base (这里其实理解为 penalize_base) 的取值范围为 [0, 1].

我们画出 bonus_base 的图象，这里 x, y 轴为 strain_time, z 轴为 bonus_base 的值:

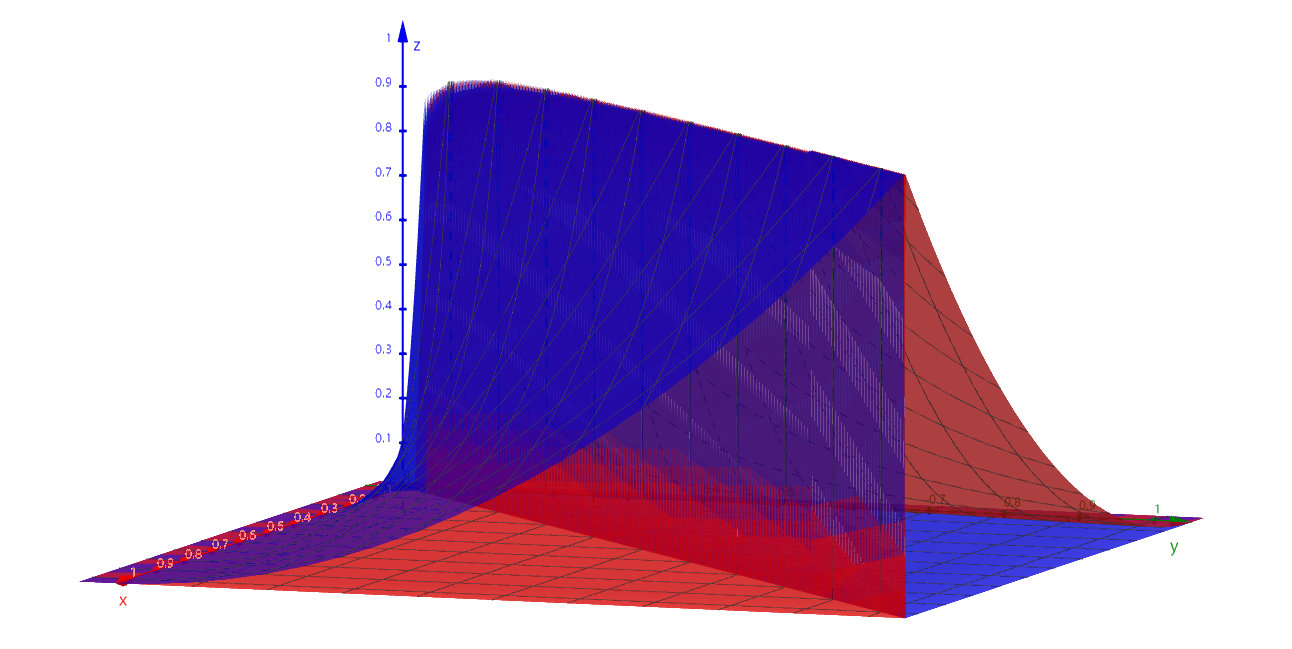
可以明显地看到，当 strain_time 不变时，几乎没有惩罚 (bonus_base 值为 1).

当 strain_time 出现变化时，我们假定一个横纵坐标，都有一个较小的 bonus_base 与其对应. 时间变化越大时，惩罚越大.

注：因为 x, y 轴 strain_time 可以等比缩放，这里都设置为了 1 方便查看.

读者可能不容易理解，为什么要针对时间变化进行惩罚呢，这里我们举出游戏中的一个例子:

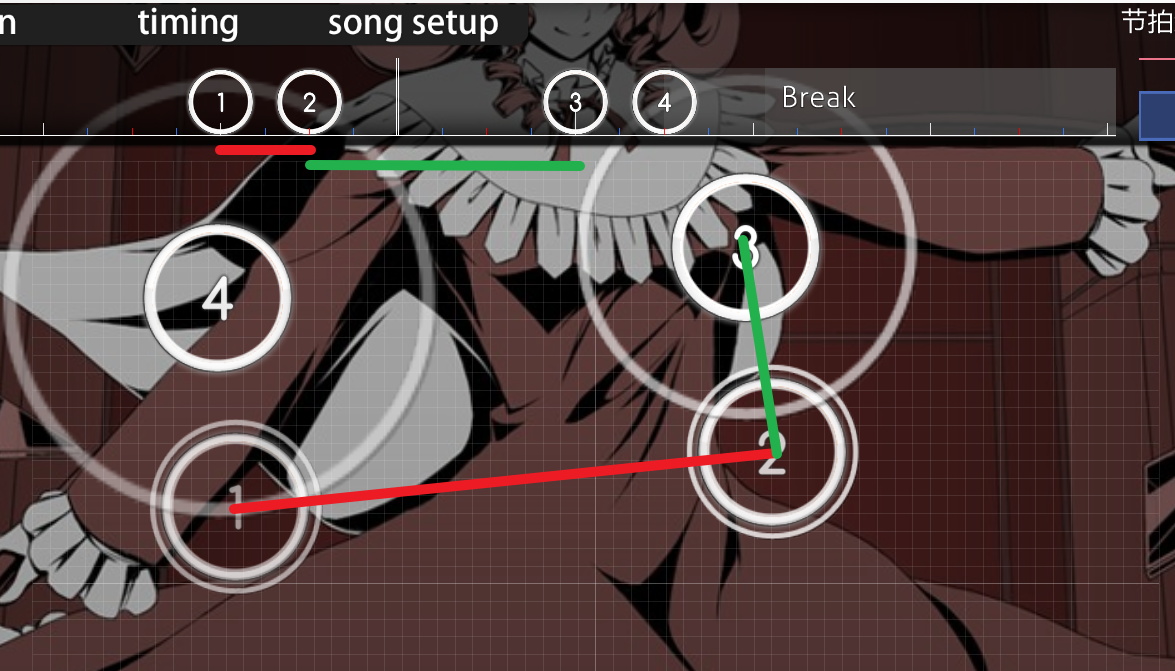
我们将圆圈 3 作为当前物件，这里圆圈 2 就是上一物件，计算圆圈 3 的速度变化奖励将利用二者的速度.

圆圈 3 的速度利用绿线计算，属于间距小时间长，速度必然很小.

圆圈 2 的速度利用红线计算，属于间距大时间短，速度必然很大.

在不引入时间变化惩罚的情况下，算法将认为圆圈 3 的难度较高，因为出现了较大的速度变化.

但实际上在玩家游玩中，因为圆圈 3 与上一物件有较长的时间间隔，所以已经感受不出速度变化了，此时圆圈 3 的难度很低.

从另一个角度来说，如果我们将 1, 2, 3, 4 的时间轴拖拽均匀，那么这是一段较难的排列，玩家点击圆圈 3 时需要一定的 aim control 能力.

# 基值 *= 奖励

if osu_last_obj.base.is_slider() {

    // * Reward sliders based on velocity.

    slider_bonus = osu_last_obj.travel_dist / osu_last_obj.travel_time;

}

// * Add in acute angle bonus or wide angle bonus + velocity change bonus, whichever is larger.

aim_strain += (acute_angle_bonus * Self::ACUTE_ANGLE_MULTIPLIER).max(

    wide_angle_bonus * Self::WIDE_ANGLE_MULTIPLIER

        + vel_change_bonus * Self::VELOCITY_CHANGE_MULTIPLIER,

);

// * Add in additional slider velocity bonus.

if with_sliders {

    aim_strain += slider_bonus * Self::SLIDER_MULTIPLIER;

}

aim_strain

在上面的部分中，我们已经将最终计算所需的各类奖励值和基础值计算好了，总算要到最终计算 aim_strain 的时刻了.

首先映入我们眼帘的是一些定义好的常量 (以全大写和下划线命名), 这些常量规定了各增益在最终计算中的占比，反应了参与计算的参数在最终数值中的权

除常量外，还有一些计算引起了我们的兴趣，第一是滑条奖励的计算，是比较简单粗暴的: 滑条距离 / 滑条时间 .

这类滑条奖励主要将作用于拥有高速长滑条的一些谱面 (类似源流懐古那种), 偏 Tech 类的基本上增益不到.

另外， aim_strain 取用锐角、广角、速度增益的方式也比较有意思，这里是取锐角 或 广角 + 速度中的较大者.

在上文我们提过，锐角增益的应用条件是很苛刻的 (300BPM 的跳，150BPM 的串), 这也导致了大部分的物件是不会吃到锐角奖励的.

在查看常量的取值后我们发现，针对锐角增益的乘数是大于广角增益的乘数的，这为一些高难度、苛刻的 Pattern 提供了更高的奖励.

简单来说，大部分的物件奖励值都来源于广角 + 速度的计算公式，一些常见的谱面甚至没有机会吃到锐角奖励.

# 探索 Speed Skill

同样的，我们首先来关注 speed.rs 中，针对 Speed 的 ISkill 实现 impl<'a> Skill<'a, Speed> , 将重点放在 strain_value_at 方法

fn strain_value_at(&mut self, curr: &'a OsuDifficultyObject<'a>) -> f64 {

    self.inner.curr_strain *= strain_decay(curr.strain_time, STRAIN_DECAY_BASE);

    self.inner.curr_strain +=

        SpeedEvaluator::evaluate_diff_of(curr, self.diff_objects, self.inner.hit_window)

            * SKILL_MULTIPLIER;

    self.inner.curr_rhythm =

        RhythmEvaluator::evaluate_diff_of(curr, self.diff_objects, self.inner.hit_window);

    let total_strain = self.inner.curr_strain * self.inner.curr_rhythm;

    self.inner.object_strains.push(total_strain);

    total_strain

}

经过粗略的阅读，我们发现了此处与上文 Aim 计算略微不同的地方。这里将 curr_strain(speed_strain) 作为基值，而 curr_rhythm 作为因数，速度与节奏复杂度相乘作为最终的值，所以我们下文主要分为 SpeedEvaluator 和 RhythmEvaluator 两个板块

此处的节奏复杂度 (RhythmEvaluator) 就是在 2021 年 11 月 Rework 由 Xexxar 引入的概念.

这次 Rework 备受关注和争议，但一定程度上避免了 Aim 成为主要获取 PP 的方式，将 osu! 从打地鼠模拟器的边缘拉了回来，下文我们会着重介绍这部分.

关于节奏复杂度的发展历史:

abraker95 曾在 2019 年提出过一套节奏复杂度的理论: On the topic of rhythmic complexity

2019 年，社区针对节奏复杂度的理解和讨论: Rhythmic Complexity

接下来，我们还是按照代码的顺序来逐个介绍每一块内容.

# SpeedEvaluator

在开始介绍 SpeedEvaluator 之前，我们先对一些概念进行补充:

hit_window : HitWindow 是完成物件打击的时间窗口期，与谱面的 OD 息息相关 (注意，rosu-pp 中所有提到的 hit_window 均为整段 hit_window, 即下面的计算公式 * 2).

在游戏内将光标悬停在左上角的谱面三维位置可以看到窗口期 (单位为 ms), osu!standard 模式有这样的计算方式:

这里推荐阅读 osu!Wiki: 判定严度 (Overall difficulty)

# 单拍？双按！

算法总是需要跟随谱师的脑洞不断更新迭代，有创新性的谱面经常能推动 PP 系统的更新，doubletapness 就是这样被引入的

引入 doubletapness 源于哪张谱面呢，请看 VCR (雾):

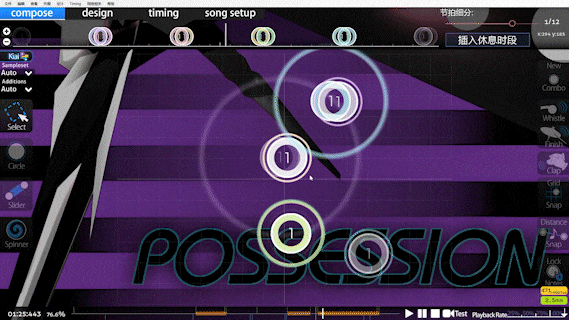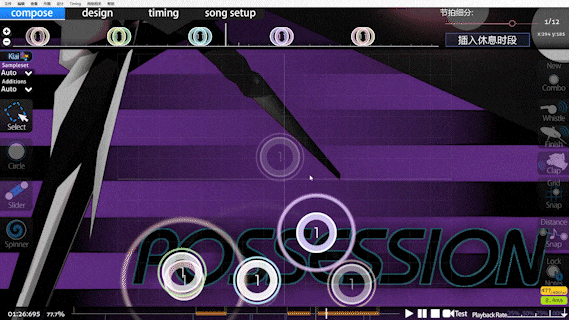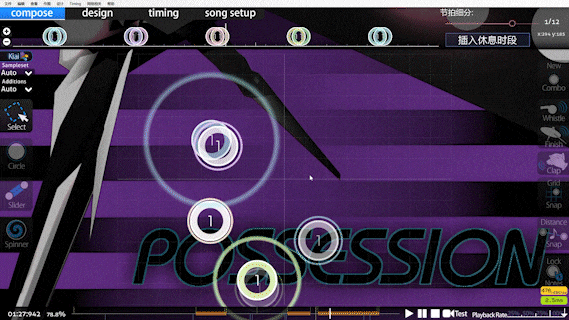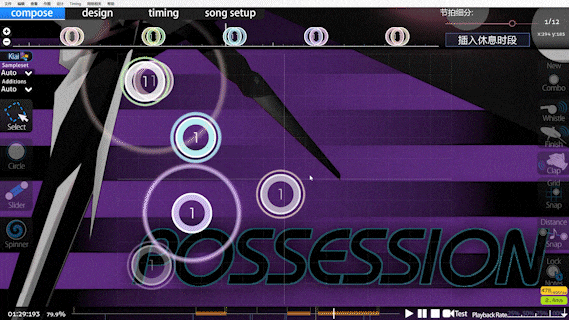
仔细看的读者应该能发现，片段中多次出现需要双按的单拍，这在 Speed 计算看来，被判定为极高速的切，DTHR 后更会使这种情况加剧.

在 doubletapness 引入之前，这张图 DTHR 后被给予了 13 星的超高难度 (目前为 8.66 星)

// * Nerf doubletappable doubles.

if let Some(osu_next_obj) = osu_next_obj {

    let curr_delta_time = osu_curr_obj.delta_time.max(1.0);

    let next_delta_time = osu_next_obj.delta_time.max(1.0);

    let delta_diff = (next_delta_time - curr_delta_time).abs();

    let speed_ratio = curr_delta_time / curr_delta_time.max(delta_diff);

    let window_ratio = (curr_delta_time / hit_window).min(1.0).powf(2.0);

    doubletapness = speed_ratio.powf(1.0 - window_ratio);

}

window_ratio 将相邻两个物件与 300 的 hit_window 相比较。假定 N 是当前物件，如果 delta(N, N-1) 比 300 的 hitwindow 小，那么在 (N-2, N-1) 与 (N-1, N) 之间可以认为存在 doubletapness 的情况，这里 window_ratio 是 doubletapness 的定性参数

delta_diff 表明了本次间隔与下次间隔之间的差值。这里我们以 GIF 中任意一个圆圈 2 举例，圆圈 2 的该值会非常大 (2 与前一个 1 之间间隔非常短，而与下一个 1 之间间隔非常长), 如果我们转而观察任意一个圆圈 1, 可以得到相同的结论。这里我们发现 delta_diff 就是衡量 doubletapness 的定量参数

speed_ratio 是衰减幅度的一部分。意在将 raw_doubletapness 归一化到当前量纲

这里提到的 300 的 hitwindow, 可以利用上文的公式: 2(80 - 6 * OD) 计算得到，这里的 2 意味着我们考虑整段 hitwindow, 包含正负段

doubletapness 由 apollo-dw 在 2022 年引入: Rework doubletap detection in osu!'s Speed evaluator

感兴趣的读者可以到 apollo-dw 提供的图形计算器自己调整参数尝试: Desmos

需要注意的是，在 2021 年前后，apollo-dw 推进了许多与 Speed 计算有关的提案，doubletapness 修复只是 apollo-dw 伟大改革的一次未雨绸缪.

apollo-dw 的名字还会在下面的内容中出现.

# 速度为底、距离为因

// * Cap deltatime to the OD 300 hitwindow.

// * 0.93 is derived from making sure 260bpm OD8 streams aren't nerfed harshly, whilst 0.92 limits the effect of the cap.

strain_time /= ((strain_time / hit_window) / 0.93).clamp(0.92, 1.0);

// * derive speedBonus for calculation

let speed_bonus = if strain_time < Self::MIN_SPEED_BONUS {

    let base = (Self::MIN_SPEED_BONUS - strain_time) / Self::SPEED_BALANCING_FACTOR;

    1.0 + 0.75 * base.powf(2.0)

} else {

    1.0

};

let travel_dist = osu_prev_obj.map_or(0.0, |obj| obj.travel_dist);

let dist = Self::SINGLE_SPACING_THRESHOLD.min(travel_dist + osu_curr_obj.min_jump_dist);

(speed_bonus + speed_bonus * (dist / Self::SINGLE_SPACING_THRESHOLD).powf(3.5))

    * doubletapness

    / strain_time

在计算的开头，我们注意到了这个对于 strain_time 的限制操作，他实际来源于 apollo-dw 的一个 commit: Remove speed caps in osu! difficulty calculation

限制 strain_time 的本意是防止高 BPM 低 OD 串的谱面算出过高的星数，同时推进移除旧算法直接限制 Speed 值的行为.

这里考虑了物件之间的间隔时间是否小于 300 的 hitwindow, 如果小于，就会对 strain_time 进行削弱.

apollo-dw 与 emu1337 通过上面提到的 doubletapness 修复和限制 strain_time 推进了 Remove speed caps in osu! difficulty calculation 提案.

在 2024 年看来，这些提案还是非常有前瞻性的，Wooting 的出现大幅提升了头部玩家的高速串能力，旧～333bpm 1/4 的限制移除是大势所趋

speed_bonus 是从 75ms 开始的 (200BPM), dist 是从 125osu!pixel 开始的，总体趋势为速度越大，距离越远，strain 值越大.

这里我们利用 matplotlib 绘制了 speed_bonus 关于 strain_time 的曲线提供给读者参考:

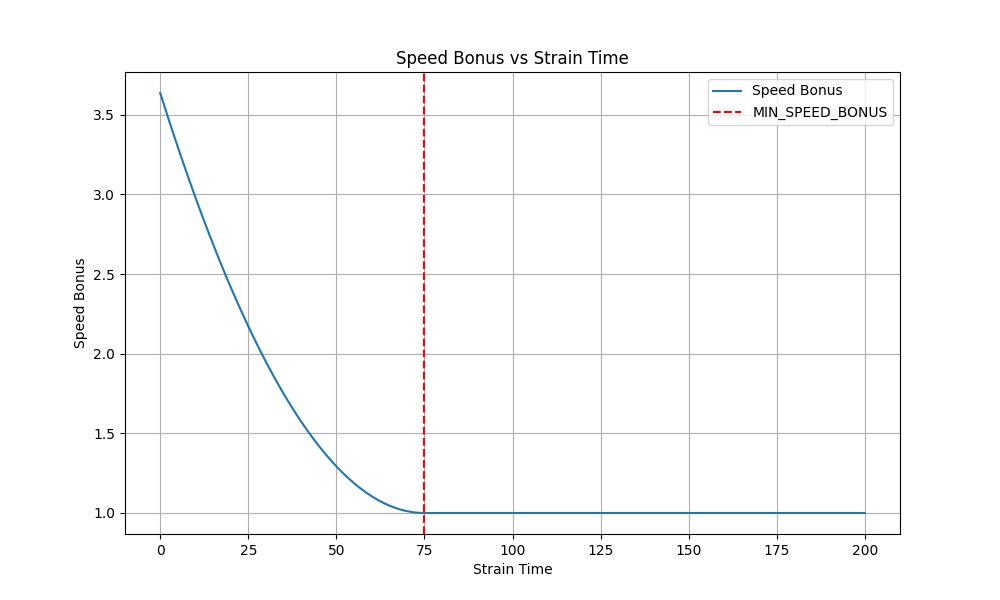
对于 dist 的计算，这里与 Aim 中的 velocity extends 概念非常相似，这里我们重新引入那张图片:

请读者将圆圈 2 当做当前物件，这里圆圈 2 的 dist 就是红色距离与橙色距离的和

# RhythmEvaluator

由于 RhythmEvaluator 较为复杂，这里我们先对原理进行总体而粗略的解释，再结合代码分析.

首先，RhythmEvaluator 本身与上文的 AimEvaluator, SpeedEvaluator 无异，都是针对具有上下文的单个物件算出的值.

节奏复杂度围绕 effectiveRatio 这个参数展开。首先，effectiveRatio 会根据初始节奏变化得到一个基值，再通过类似组间评分的方式进行削弱.

# 组间评分

这里，我们利用比较通俗的语言模拟一下组间评分的过程:

首先，先寻找当前物件 5s 内的 0~32 个历史物件，最终会脱颖而出 rhythmStart 个历史物件

接下来，我们会按顺序遍历这些个历史物件，尝试在遍历中对前后相邻的物件进行分组 ( island ), 分组依据是节奏发生了较大幅度变化 ( deltaTime 变化超出 25%)

遍历过后，所有的历史物件都应该被分好了自己的小组 ( island ), 小组人数为 1~8 人。小组可以容纳超过 8 个物件，但小组人数只会被记作 8

最后，我们要在小组 ( island ) 间进行评分，当某些 Pattern 出现时， effectiveRatio 值会被削弱，例如：人数相等的小组重复出现 (xxx-xxx), 前后小组人数奇偶相同 (xx-xxxx) 等等

示意图 (图片部分来自 emu1337 的截图):

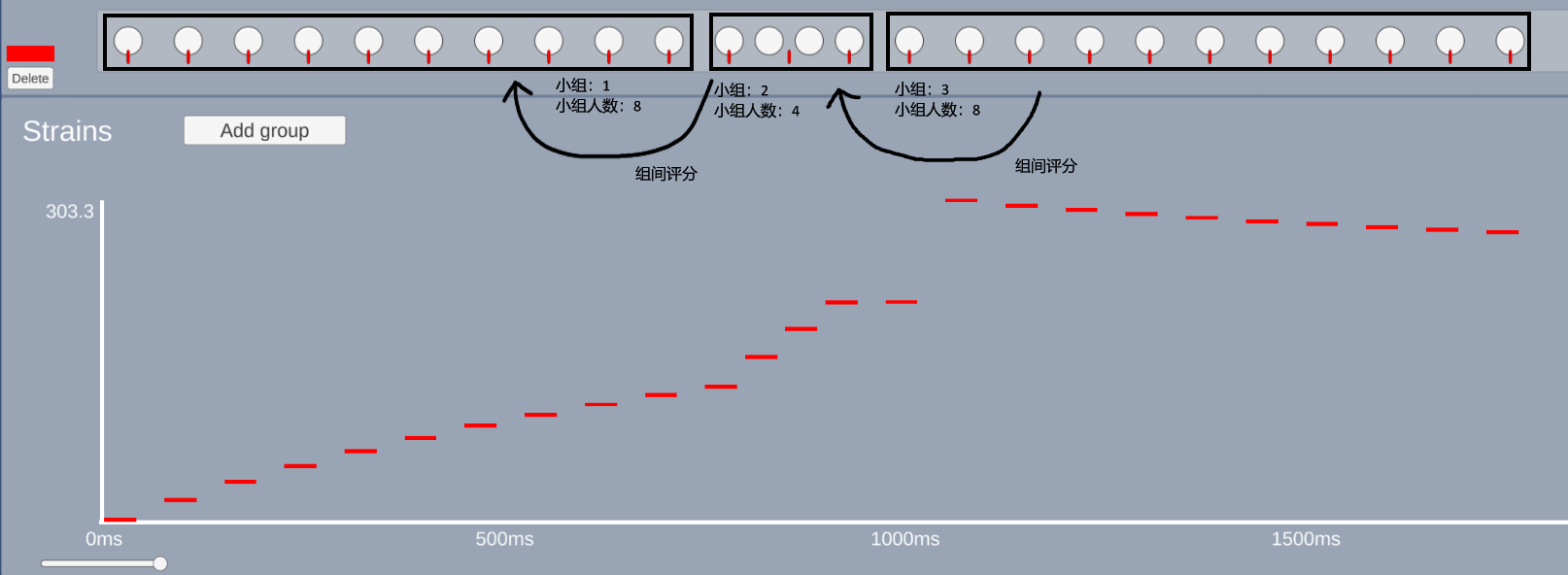
# 实现细节

接下来我们将结合代码对提到的组间评分过程进行分析，需要注意的是，这里为了提高可读性，选择了 C# 版本的代码.

# 筛选对象

int historicalNoteCount = Math.Min(current.Index, 32);

int rhythmStart = 0;

while (rhythmStart < historicalNoteCount - 2 && current.StartTime - current.Previous(rhythmStart).StartTime < history_time_max)

    rhythmStart++;

相信这里看到 rhythmStart , 读者应该并不陌生，我们在此处完成了寻找当前物件 5s 内的 0~32 个历史物件的操作.

# 进行分组

for (int i = rhythmStart; i > 0; i--)

{

    // 省略了 effectiveRatio 初值的计算

    if (firstDeltaSwitch)

    {

        if (!(prevDelta > 1.25 * currDelta || prevDelta * 1.25 < currDelta))

        {

            if (islandSize < 7)

                islandSize++; // island is still progressing, count size.

        }

        else

        {

            // 省略了对于 effectiveRatio 的削弱计算

            /*

                将分组运算的结果累计到 rhythmComplexitySum 中，后文我们会再提到

                rhythmComplexitySum += Math.Sqrt (effectiveRatio * previousRatio) * currHistoricalDecay * Math.Sqrt (4 + islandSize) / 2 * Math.Sqrt (4 + previousIslandSize) / 2;

                previousRatio = effectiveRatio;

            */

            previousIslandSize = islandSize; // log the last island size.

            if (prevDelta * 1.25 < currDelta) // we're slowing down, stop counting

                firstDeltaSwitch = false; // if we're speeding up, this stays true and we keep counting island size.

            islandSize = 1;

        }

    }

    else if (prevDelta > 1.25 * currDelta) // we want to be speeding up.

    {

        // Begin counting island until we change speed again.

        firstDeltaSwitch = true;

        previousRatio = effectiveRatio;

        islandSize = 1;

    }

}

此处的代码段省略了部分值的计算过程，让我们聚焦于 island 的分组依据和分组过程.

首先，for 循环让我们对所有的历史物件遍历，显而易见的， firstDeltaSwitch 是新小组产生的定性判据.

一旦满足 prevDelta > 1.25 * currDelta , 即 deltaTime 发生了加速 25% 的变化时，算法认为应该生成一个新的小组了.

在下一次循环中，由于 firstDeltaSwitch 被置为 true , 算法将走入第一个 if 分支中.

显然，第二个 if 分支决定了分组结果，一旦 prevDelta > 1.25 * currDelta || prevDelta * 1.25 < currDelta 条件满足，即速度发生了较大变化时，当前小组将结束并进行结算 (else 分支).

结算的过程就是我们在上文提到的小组 ( island ) 间进行评分的过程。与伪代码描述不同的是，在真实代码中，分组与结算是接连完成的，而不是先分组再结算的.

很明显地，结算时我们有意地储存了一些 previousIsland 的状态，不难理解，这是在为下一小组结算时创建上下文

另外地，这里 if (prevDelta * 1.25 < currDelta) firstDeltaSwitch = false; 当速度维持上涨趋势时，小组可以接连被创建。当速度不再上涨时，定性判据将被复原，直至下一次满足 prevDelta > 1.25 * currDelta

敏锐的读者可能察觉到我们上文示意图中的错误，实际上，单调节奏不是被分为了一个大组，而是很多人数为 1 的小组.

# 初值计算

double currHistoricalDecay = (history_time_max - (current.StartTime - currObj.StartTime)) / history_time_max; // scales note 0 to 1 from history to now

currHistoricalDecay = Math.Min((double)(historicalNoteCount - i) / historicalNoteCount, currHistoricalDecay); // either we're limited by time or limited by object count.

double currRatio = 1.0 + 6.0 * Math.Min(0.5, Math.Pow(Math.Sin(Math.PI / (Math.Min(prevDelta, currDelta) / Math.Max(prevDelta, currDelta))), 2)); // fancy function to calculate rhythmbonuses.

double windowPenalty = Math.Min(1, Math.Max(0, Math.Abs(prevDelta - currDelta) - currObj.HitWindowGreat * 0.3) / (currObj.HitWindowGreat * 0.3));

windowPenalty = Math.Min(1, windowPenalty);

double effectiveRatio = windowPenalty * currRatio;

# currHistoricalDecay

在进行分组部分的代码展示中，我们一笔带过了 rhythmComplexitySum 的计算，其中引用了 currHistoricalDecay 这个概念.

重新审视整个过程，我们会针对每一个物件应用 RhythmEvaluator, 在单一物件中提出 Sum 这种概念是很危险的，我们需要将 Sum 平摊到每一个物件的 strain 上.

最简单的方式是直接将 rhythmComplexitySum 除以 rhythmStart , 但这样显然并不明智。所以在这里引入了 currHistoricalDecay .

currHistoricalDecay 根据相差时间进行均匀的伸缩，把 Sum 值平摊到 0~N 个历史物件中.

# effectiveRatio

currRatio 的表达式我们并不陌生，

currRatio 的函数表达形式 (先正弦再平方) 我们并不陌生，与 Aim 中曾提到的速度变化奖励不能说毫不相干，只能说一模一样.

这里我们甚至可以引用上文的原文:

(prev_vel - curr_vel).abs() / prev_vel.max(curr_vel) 计算了速度变化的大小相对于最大速度的比例，反应了速度变化的剧烈程度.

相同地，这里也采用了先正弦再平方的方式进行因数的归一化，有疑问的读者可以返回上文查看.

Xexxar 也放出了该公式的图形计算器: Desmos

windowPenalty 主要针对重叠的窗口进行惩罚，这里的玩法类似于之前 apollo-dw 的 doubletapness .

# 组间计算

if (currObj.BaseObject is Slider) // bpm change is into slider, this is easy acc window

    effectiveRatio *= 0.125;

if (prevObj.BaseObject is Slider) // bpm change was from a slider, this is easier typically than circle -> circle

    effectiveRatio *= 0.25;

if (previousIslandSize == islandSize) // repeated island size (ex: triplet -> triplet)

    effectiveRatio *= 0.25;

if (previousIslandSize % 2 == islandSize % 2) // repeated island polartiy (2 -> 4, 3 -> 5)

    effectiveRatio *= 0.50;

if (lastDelta > prevDelta + 10 && prevDelta > currDelta + 10) // previous increase happened a note ago, 1/1->1/2-1/4, dont want to buff this.

    effectiveRatio *= 0.125;

通过简单的阅读，我们很容易发现组间削弱的逻辑，同时我们也逐渐意识到节奏分组的优势与可行性所在.

至此，我们已经通过 AimEvaluator 和 SpeedEvaluator 探索了 osu! 算法的设计逻辑和具体实现。在探究的过程中，笔者希望读者在满足了好奇心的同时，对于音乐类游戏的算法体系有一些简单的理解和感悟。在行文过程中，我们也涉及到了诸如函数拟合、归一化等统计学知识，希望对于启发读者进行数学相关研究有帮助.

2024-07-01 至 2024-09-19, 兔肉献上.